Les tableaux▲
But de ce chapitre▲
Jusque là , nous n'avons que très peu de moyens de représenter les données d'un programme. Une donnée en mémoire est soit une variable de type Integer, soit une variable de type Double, String ou Boolean. Pour chaque donnée du programme, nous avons donc ainsi une unique variable.
En réalité, comme nous allons le voir dans ce cours et le suivant (cours concernant les types structurés), une même variable peut contenir un ensemble de données. En particulier, lorsque toutes ces données sont de même type, il est possible de les stocker dans une variable de type tableau.
L'objectif de ce cours est de vous apprendre à définir et à utiliser cette nouvelle manière de représenter les données.
Les tableaux Ă une dimension▲
Exemple introductif▲
Supposons qu'on ait le problème suivant : on voudrait écrire une procédure permettant de multiplier dix nombres entiers par 3.
Les dix entiers sont des variables globales. Il faut donc tout d'abord déclarer dix variables globales :
Var N1, N2, ..., N10 : Integer;Et la procédure de multiplication devrait comporter dix instructions :
Procedure MultiplierPar3 ();
Begin
N1 := N1 * 3;
N2 := N2 * 3;
.
.
N10 := N10 * 3;
End;Pour dix entiers, cette manière de procéder est envisageable. Mais imaginez qu'on ait le même problème avec un million d'entiers !
Ne croyez pas, d'ailleurs, que le traitement d'un million d'entiers soit un problème totalement irréaliste, car les ordinateurs ont souvent à traiter des millions de nombres en même temps. En informatique, ce type de problème est tout à fait courant.
Malheureusement, on ne peut pas utiliser de boucle pour faire ceci, car on n'a aucun moyen de faire varier le nom d'une variable !
On aurait envie d'écrire quelque chose du genre :
Var i : Integer;
For i:=1 To 10 Do Var Ni : Integer;
Procedure MultiplierPar3 ();
Var i : Integer;
Begin
For i := 1 To 10 Do Ni := Ni * 3;
End;en pensant que Ni serait successivement remplacé par N1, N2, … , N10.
Malheureusement, ce mécanisme de génération automatique de nom de variable n'est pas possible !
Alors, comment faire ?
La solution est d'utiliser un tableau.
Pour utiliser un tableau, il faut tout d'abord déclarer une variable de type tableau.
Avec l'exemple précédent, ce serait :
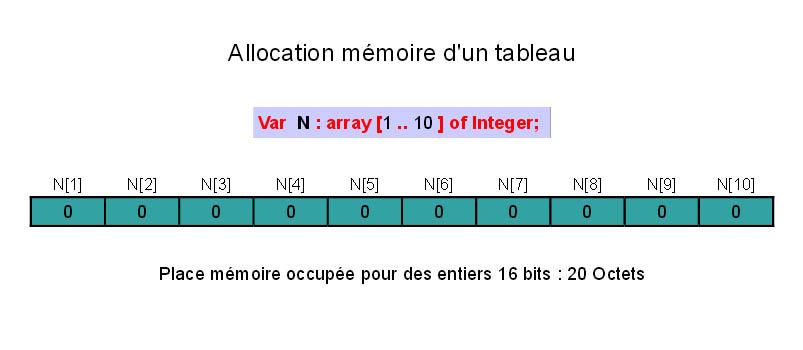
Var N : array [1 .. 10] Of Integer;Cette écriture revient à déclarer dix entiers N1, N2, … , N10, mais elle est beaucoup plus concise. Lorsqu'un interpréteur ou un compilateur rencontre une déclaration de tableau dans un programme, il alloue de la mémoire pour l'ensemble du tableau. Dans notre exemple, il y aurait donc une allocation mémoire de 20 octets en supposant des entiers 16 bits :
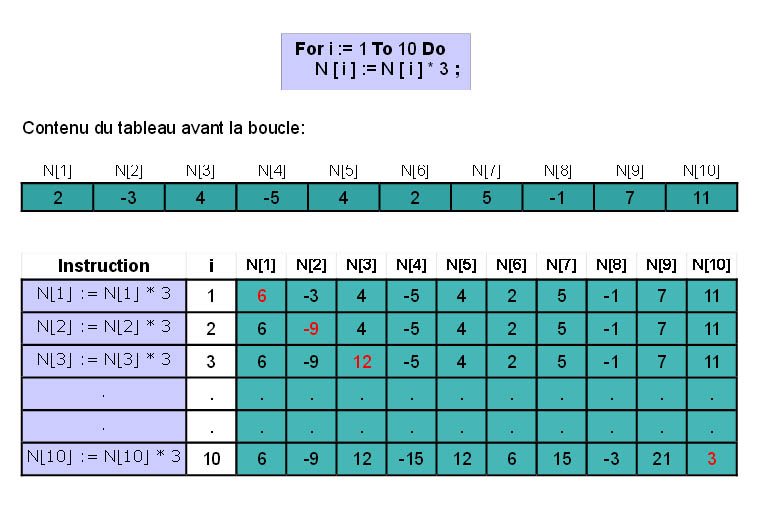
D'autre part, il devient à présent possible de multiplier les dix entiers du tableau par 3 avec une boucle For, comme ceci :
Procedure MultiplierPar3 ();
Var i : Integer;
Begin
For i := 1 To 10 Do N[i] := N[i] * 3;
End;L'écriture N[i] désigne le ième élément du tableau, autrement dit l'élément d'indice i du tableau N.
Vous constaterez qu'avec un million d'entiers, le code du programme n'est pas plus long :
Var N : array [1 .. 1000000] of Integer;
Procedure MultiplierPar3 ();
Var i : Integer;
Begin
For i := 1 To 1000000 Do N[i] := N[i] * 3;
End;Le cas gĂ©nĂ©ral▲
En Pascal, la déclaration d'un tableau s'écrit :
Var nom du tableau
: array [indice min .. indice max] Of type des éléments;où indice min et indice max sont deux entiers qui représentent respectivement le plus petit indice et le plus grand indice des éléments du tableau.
Le type des éléments peut varier d'un tableau à l'autre, mais tous les éléments d'un même tableau sont forcément du même type.
Voici, par exemple, la déclaration d'un tableau de chaînes de caractères :
Var Prenom : array [1..1000 ] Of String;On pourra ensuite affecter une valeur à un élément du tableau, tout comme on affecte une valeur à une variable. Par exemple l'instruction :
Prenom[3] := 'Jeanne';affecte la chaîne de caractères 'Jeanne' à l'élément d'indice 3 du tableau Prenom.
Utilisation de constantes pour dĂ©finir la dimension d'un tableau▲
Supposons que vous ayez à modifier un programme très long (plusieurs milliers de lignes, par exemple), qui utilise un tableau de T de dix entiers déclaré par :
Var T : array [1 .. 10] Of Integer;On vous demande de changer la dimension du tableau T de 10 Ă 20.
Supposons que dans ce programme figurent des centaines d'instructions faisant référence à la dimension du tableau T, c'est-à -dire au nombre 10.
Dans toutes ces instructions, il va donc falloir remplacer le nombre 10 par le nombre 20.
Les constantes servent en particulier Ă Ă©viter ce genre de manipulation longue et fastidieuse.
Supposons à présent que le programme initial ait été écrit en utilisant une constante DIMENSION, qui représente le nombre d'éléments du tableau T, déclarée comme suit :
Const DIMENSION = 10;et que le tableau soit déclaré comme suit :
Var T : array [1..DIMENSION] of Integer;Si le développeur qui a écrit le programme a bien fait les choses, il aura fait référence à la constante DIMENSION (et non pas 10 !) dans toutes les instructions utilisant la dimension du tableau T.
Un programme écrit de cette manière est beaucoup plus facile à mettre à jour. En effet, pour changer la dimension du tableau de 10 à 20, il vous suffit à présent de modifier une seule ligne de programme : la déclaration de la constante DIMENSION. c'est-à -dire que vous allez la remplacer par :
Const DIMENSION = 20;et tout le reste fonctionnera tout seul !
Vous vous demandez peut-être pourquoi on n'aurait pas pu utiliser une variable à la place de la constante. c'est-à -dire déclarer :
Var DIMENSION : Integer;
T : array [1..DIMENSION] of Integer;puis faire DIMENSION := 10; au début du programme.
Ceci ne fonctionne pas !
Pourquoi ?
Parce que la dimension d'un tableau ne peut pas être modifiée pendant l'exécution d'un programme.
En effet, un tableau est un objet statique, c'est-à -dire que l'espace mémoire qui lui est alloué ne peut être modifié en cours d'exécution.
Cela présente un certain nombre d'inconvénients. En particulier, si vous ne connaissez pas a priori la taille de tableau qu'il vous faudra pour résoudre un problème particulier, la seule solution que vous avez est de prévoir large, de manière à ce que vous ne risquiez pas d'avoir un dépassement de capacité (taille de tableau insuffisante pour enregistrer toutes les données).
Nous verrons ultérieurement qu'il existe d'autres manières de représenter les informations en mémoire (on parle de structures de données), qui permettent d'éviter ce problème.
Tableaux remplis partiellement▲
ReprĂ©sentation▲
Nous avons vu qu'un tableau est un objet statique, c'est-à -dire que sa dimension ne peut pas être modifiée pendant l'exécution d'un programme.
Il faut donc toujours prévoir large, c'est-à -dire déclarer un tableau de taille suffisante pour tous les cas de figure.
Cela signifie que l'on va, en général, remplir les tableaux partiellement jusqu'à un certain indice définissant la fin des données.
Pour représenter un tableau rempli partiellement, il faut donc nécessairement une variable entière qui contiendra à tout moment l'indice de fin des données.
Pour fixer les idées, prenons une variable T pour le tableau et une variable N pour l'indice de fin. On aura donc les déclarations suivantes :
Const M = Nombre maximum d'éléments;
Var N : Integer;
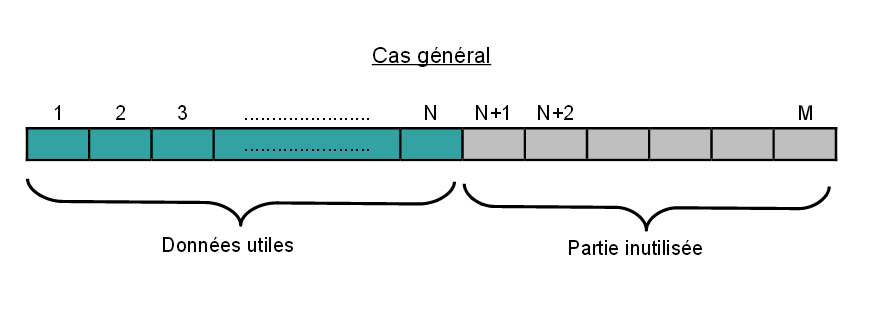
T : array [1..M] of Type;Les données utiles sont stockées dans les N premiers éléments du tableau :
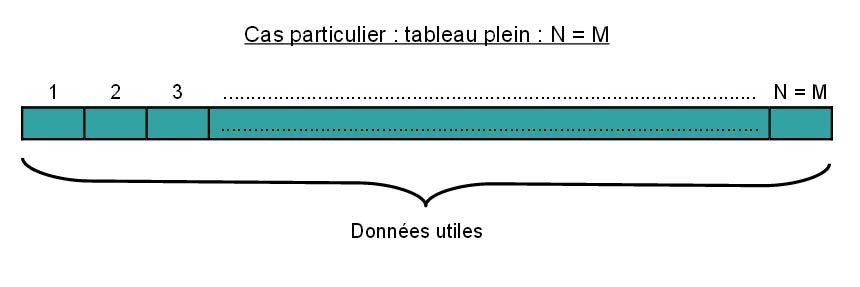
Le tableau est « vide » lorsque N vaut 0 et plein lorsque N est égal à M :
Adjonction d'une valeur▲
Adjonction Ă la fin▲
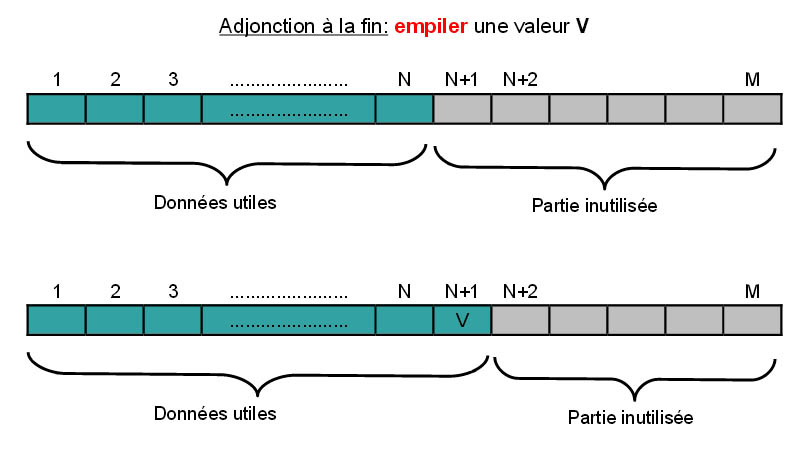
Pour ajouter une valeur V à un tableau rempli partiellement, le plus simple est de l'ajouter à la fin. On appelle cette opération empiler. L'élément qui suit le dernier prend la valeur V et l'indice de fin est incrémenté :
T [N+1] := V;
N := N+1;Insertion▲
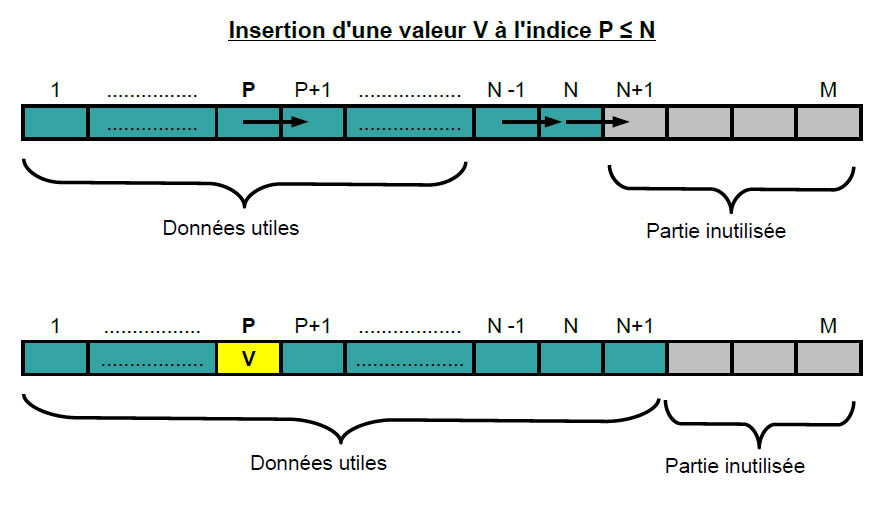
Insérer une valeur dans un tableau est une opération plus complexe. Supposons que l'on souhaite insérer une valeur V à l'indice P (P ≤ N) du tableau. Il faut d'abord « faire de la place » pour cette nouvelle valeur, c'est-à -dire décaler toutes les valeurs entre les indices P et N, d'un cran vers la droite. La valeur V peut ensuite être affectée à l'élément d'indice P. Puis, comme on a ajouté une valeur, l'indice de fin augmente de 1 :
For i := N DownTo P Do T[i+1] := T[i];
T[P] := V;
N := N+1;Suppression d'un Ă©lĂ©ment▲
Suppression du dernier Ă©lĂ©ment▲
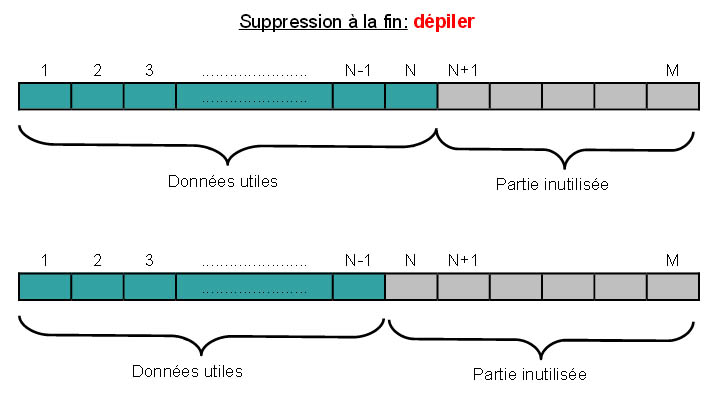
Le dernier élément d'un tableau est le plus simple à supprimer ; pour cela, il suffit de dépiler, c'est-à -dire de décrémenter l'indice de fin de 1 :
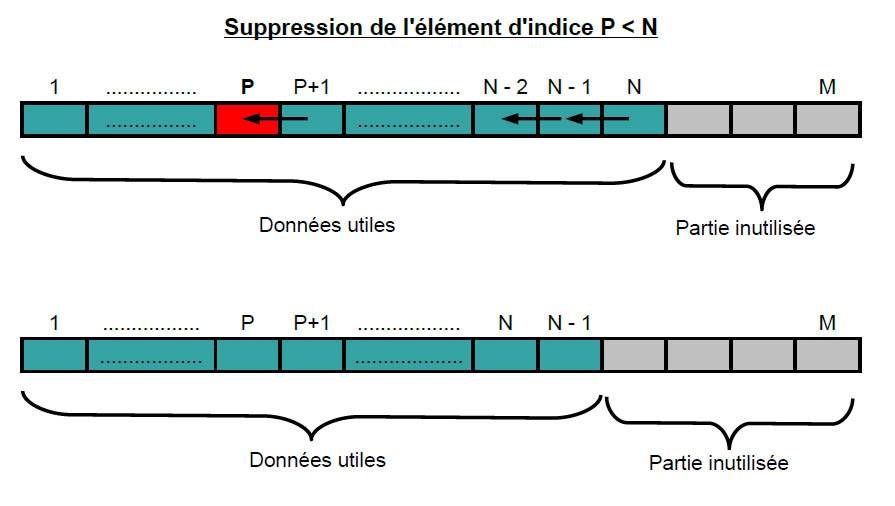
N := N - 1;Suppression d'un Ă©lĂ©ment quelconque (diffĂ©rent du dernier)▲
Notion de pile▲
Un tableau rempli partiellement sur lequel on ne fait que des opérations empiler et dépiler est une structure de données fondamentale de l'informatique que l'on appelle une pile (stack en anglais).
En particulier, la gestion mémoire des variables locales et des paramètres des sous-programmes utilise une pile : les valeurs des variables sont empilées lorsque l'on rentre dans le sous-programme et dépilées à la sortie.
Les tableaux Ă deux dimensions▲
DĂ©claration en Pascal▲
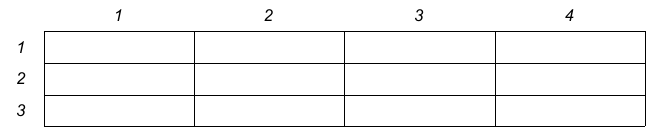
var T : array [ 1..3,1..4 ] of integer;T [ i , j ] est l'élément de T se trouvant à la ligne i et à la colonne j.
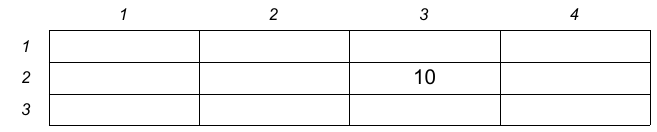
Exemple : T [2, 3] := 10;
Traitement de tous les Ă©lĂ©ments▲
Principe :
for i := 1 to 3 do
begin
for j := 1 to 4 do
begin
Traitement de l'élément T[ i, j ]
end
endExemple :
for i := 1 to 3 do
begin
for j := 1 to 4 do
begin
T [ i , j ] := j + 3 * (i - 1) ;
end
endTraitement d'une ligne▲
Principe : traitement de la ligne i :
for j := 1 to 4 do
begin
Traitement de l'élément T[ i, j ]
endExemple : traitement de la ligne 2 :
for j:= 1 to 4 do
begin
T [2, j ] := 2 * j ;
endTraitement d'une colonne▲
Exercices▲
Retrouvez les énoncés d'exercices sur le site de l'auteur :
- les tableaux à une dimension :
- tableaux remplis partiellement ;
- les tableaux Ă deux dimensions.
Pour obtenir les corrigés, le téléchargement n'est possible que via un login et un mot de passe, que vous pouvez obtenir en envoyant un mail à l'adresse suivante :

en précisant un peu qui vous êtes et les raisons pour lesquelles ce cours vous intéresse.